This page is supposed to follow on from the one on meantones. Schismic scales are less well known than meantones, so I'll try to assume less knowledge here than in that other page. Here's your menu:
Melodic Definition of Schismic Scales
Schismic scales, like meantones, can be defined in terms of a 12 note scale. However, whereas meantones are 7+5 scales, schismic scales are 5+7. So, what's the difference? Schismic scales have 5 large and 7 small intervals whereas it's the other way round for meantones. I'm going to define the larger semitone as σ and the smaller one as ρ.
By this definition, Pythagorean temperament is schismic. If you treat it as a meantone, you end up with this diatonic scale:
| C | D | E | F | G | A | B | C | |||||||
| τ | τ | ρ | τ | τ | τ | ρ |
Where τ=σ+ρ That means ρ is the equivalent of the meantone s, and so is sometimes called a diatonic semitone. More commonly, it's called a limma.
As schismic scales are composed of 12 semitones, you can fit them to a 12 note keyboard. Here's my preferred mapping:
| C | C# | D | Eb | E | F | F# | G | GA | A | Bb | B | C | ||||||||||||
| ρ | σ | ρ | ρ | σ | ρ | σ | ρ | ρ | σ | ρ | σ |
The reasons for this particular mapping will become clear by the end of the page. Notice I'm using the traditional names for the 12 notes. They are only really valid for meantones, but there's no need to hit you with a radically new notation when you're still being introduced to the concepts. There's no distinction between 12 note enharmonies. So, you could replace C# with Db without changing the scale. I'm using these names as they make some sense of the σ and ρ's, and because they're the one's you have with the simplest meantone mapping. As the G#/Ab note is ambiguous in 12 note meantone, I'm calling it GA for brevity and neutrality.
The mapping I've just given is defined from the spiral of fifths around GA. Why GA? Because it's a point of symmetry on a standard keyboard. So why not D? Patience, all will be revealed in due course.
With meantones, it was really easy to write down the spiral of fifths, because there's a popular notation implicitly based around meantones. Here, though, that's not so easy. So, I'll have to devise a notation based around the spiral of fifths instead.
Schismically speaking, 12 fifths are sharp of 7 octaves by one comma . If the fifths are just, it'll be a Pythagorean comma. In general, though, it's always some kind of comma. It also happens to be the difference between the two kinds of semitone. I'll give it the symbol π so we can say π=σ-ρ. This is the equivalent of the meantone interval I called q.
To write any schismic interval, we can specify the number of commas it is sharp or flat of one of the 12 fixed notes I defined above. I'll keep the same note names, and use / to mean raise by a comma and \ to mean lower by a comma. Don't get confused with the same intervals I sometimes use to raise or lower by the meantone q. Here, then, is a chunk of the spiral of fifths around GA:
Note that there are 5 notes to the left of GA, but 6 to the right. This means that the tuning of D is ambiguous with 12 notes from the spiral of fifths around GA, the same say that GA is in the spiral around D I used for meantone. Some readers may happen to know that D usually needs to take on 2 values in the key of C major. The difference between them is a comma. It's no coincidence that the same thing's happening here. But I'm getting ahead of myself.
You could have the black notes close to Pythagorean, and average the white notes to equalize the two tones. This is the key to a lot of well temperaments. For example, Werckmeister III has all fifths between black notes and a couple more as Pythagorean.
Have some more fifths, they're going cheap!
Singly Positive Linear Temperaments
The normal distinction between positive and negative temperaments is the same as my distinction between meantones and schismic scales. However, whereas meantones can be either singly or doubly negative, schismic scales are much more consistently singly positive.
The positivity of an equal temperament is the number of steps in its equivalent of the Pythagorean comma. For schismic scales, this is that general comma π. (For meantones, it comes out as -q, from which follows their negativity.) As explained on another page, double positive scales smaller than 94-equal aren't really schismic, although they can be described as such if you really want. So, the terms "singly positive" and "schismic" are roughly synonymous.
The pattern of singly positive scales is 5+12n. That gives the set 5, 17, 29, 41, 53, 65, 77, ...
So, 5-equal is the first schismic scale, like 7 is the first meantone. This all connects with the meantone spiral of fifths centering on the white notes, and the schismic spiral centering on the black notes.
Approximations to Just Intonation
Oh yes, this is the moment you've all been waiting for! Although schismic scales can be derived and notated with no mention of the overtone series, it's their close match to just intonation that provides their raison d'être.
In schismic scales, a third is associated with 8 fourths rather than 4 fifths. This means you need more notes to cover any given set of scales than you do for meantone.
Also, as you may already know or have guessed, there is a difference between major and minor tones in schismic temperament. Therefore, you can't cover all the chords of a diatonic scale with only 7 notes. Partly, of course this is bad. It does bring you closer in touch with "acoustic reality" though. It means composing in schismic temperament is that bit closer to just intonation. Also, there should be less ambiguity for a dynamic tuning algorithm converting from ST to JI.
To explain how schismic temperament works, here's a chunk of the 7-limit lattice using the notation I defined above:
B\-------F#\-------C#\-------GA\-------Eb\-------Bb\
\ / \ / \ / \ / \ /
\ GA / \ Eb / \ Bb / \ F / \ C /
\ / C\\ \ / G\\ \ / D\\ \ / A\ \ /
\ / \ / \ / \ / \ /
D\--------A---------E---------B---------F#
/ \ / \ / \ / \ / \
/ \ B/ / \ F#/ / \ C#/ / \ GA/ / \
/ GA\ \ / Eb\ \ / Bb\ \ / F\ \ / C\ \
/ \ / \ / \ / \ / \
Bb--------F---------C---------G---------D---------A/
\ / \ / \ / \ / \ /
\ G/ / \ D/ / \ A// / \ E// / \ B// /
\ / B \ / F# \ / C# \ / GA \ /
\ / \ / \ / \ / \ /
C#/-------GA/-------Eb/-------Bb/--------F
To get all those notes, I reckon you need 42 steps from the spiral of fifths. I hope that makes some sense. Another approach is to go back to the standard scale
| C | C# | D | Eb | E | F | F# | G | GA | A | Bb | B | C | ||||||||||||
| ρ | σ | ρ | ρ | σ | ρ | σ | ρ | ρ | σ | ρ | σ |
and list some 5-limit chords that are in tune:
The major third splits in two different sized tones. The larger is τ=σ+ρ that we've met before. The smaller is 2ρ. So, you could also write the minor third as τ+s. The difference between the two tones is σ+ρ-2ρ = σ-ρ = π. So, the two tones are separated by our general comma, which can therefore be identified with a syntonic comma as well as a Pythagorean one. It can be a septimal comma as well. See why I call it a comma?
The 7-limit schismic approximation less well known. Erv Wilson hit on it back in 1975, in his "Keyboarding Genus 41".
The page on my fourth based keyboard mapping tells you how to play 7-limit chords.
Oh, I don't know. I can't be bothered to do a whistle stop tour like I did with meantones. Have a look at the schismic fourth tuning page to see how you can get to hear at least one schismic scale.
For different tunings, well, 53-equal is good in the 5-limit, but I find the small intervals too small. -1/8-schisma (where the fifth is flat by one eighth of the difference between a Pythagorean and syntonic comma) is so close to 5-limit JI as to be almost indistinguishable. 118-equal is almost as perfect. It has a moderately good 7-limit approximation as well, but you really need all 118 notes to get it to work.
Also, try 41-equal. And 17 and 29 if you like.
Plus, remember that 12-equal is as much schismic as it's a meantone.
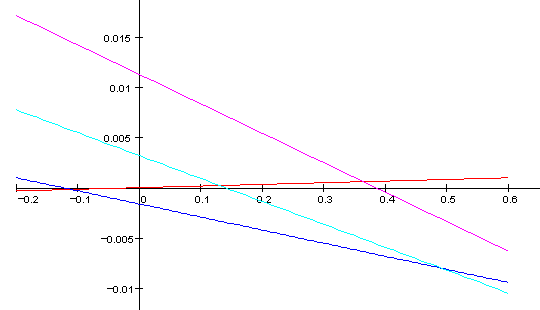
Oh yes! No music to bother us now, only some semi-applied mathematics. Here's a graph:

The y (vertical) axis shows how sharp an interval is. The x axis shows the k-schisma parameter alluded to before. This is how sharp the fifth is from just in terms of schisma. That is, the difference between the Pythagorean and syntonic commas -- a paltry 2 cents. Remember the sign on k (I usually do!) because fifths can be sharp as well as flat here.
The red line shows how sharp the fifth (3/2) is. The blue line shows how sharp the major third (5/4) is. The cyan line shows how sharp the subminor seventh (7/4) is. The magenta line shows how sharp the super fourth (11/8) is.
So far, so like the equivalent graphs for meantone. Note that fifths can be either sharp or flat for schismic scales. Also, the amount of tempering of the fifth is very small. This means Pythagorean tuning is a typical schismic temperament. Whereas in meantones the 5/4 and 7/4 both optimize close to 1/4-comma, schismically they lead to completely different regions. So, there's no universal "best" scale.
53-equal is at -0.035-schisma, so getting towards the 5-limit optimum. The blue line crosses the x-axis at -1/8-schisma. See what I mean about it being indistinguishable from 5-limit JI? 118-equal is ever so slightly further along. It's 7-limit approximation is better than it looks here (it's too far along the spiral of fifths to be much use in unequal temperaments).
29-equal is off the right end of the graph, and 17-equal is way off.
41-equal is about +1/4-comma schisma. So, beyond the best 7-limit approximation but better in the 11-limit. This section is supposed to be about the 11-limit after all.
Well, like with meantones, there isn't a single 11-limit approximation that works for all schismic scales. The one that last graph was drawn with is the simplest, and so the best all-round approximation. However, there's also this:
That gives you good approximations to all primes other than 5 (which still isn't that bad) for a particular range of scales. Trouble is, the 11/8 ends up quite distant on the spiral of fifths. So, you need a lot of notes to get it to work. More on this in the next section.
If you happen to be using my schismic fourth mapping, here's how you can get some chords from this approximation. Note names refer to the keys rather than schismic notes. A ' means the note is at least an octave higher than the first note in the chord. A '' means at least 2 octaves higher.
Here's the normal schismic conversion matrix:
( 1 0)
( 0 1)
C = (15 -8)
(25 -14)
(32 -18)
You can derive it by setting the Pythagorean comma (-19 12)H', the syntonic comma (-4 4 -1)H', the septimal comma (6 -2 0 -1)H' and an 11-limit comma (-1 2 0 -2 1)H' all equal to each other.
That means, to get a complete 11-limit chord, you need a string of at least 20 fifths. Even for a complete 7-limit chord, you need 16 fifths. My fourth based keyboard mapping is equivalent to 29 notes per octave, so there are plenty of either to play with. Even 29 notes aren't enough for a complete 11-limit chord in this monstrosity:
( 1 0)
( 0 1)
C = ( 15 -8)
( 25 -14)
(-33 23)
That's what the second graph I showed you was produced with. 37 fifths for one complete chord! Even if they are really good, that's quite a lot to keep track of. You see why the list of chords above is so short!
The first matrix is consistent with 41 and 29-equal, the second with 53 and 41. For 17-equal, you need yet another matrix with the bottom row (-14 11). This is a lot of hassle, as the neutral thirds are supposed to be one of the good things about 17-equal.
The "schisma" that schismic scales are named after is an interval equal to the difference between the Pythagorean and syntonic commas.It comes out as (-15 8 1)H which is some horrible ratio, and a mere 2 cents. To get the hang of the 7-limit tempering, people like the idea of a septimal schisma. The intervals 225/224 or (-5 2 2 -1)H and 5120/5103 or (10 -6 1 -1)H both fit the bill.
225/224 is 7.7 cents. It's notable in that almost all good 7-limit temperaments make this comma vanish. Some scales where it doesn't are 26-, 46- and 118-equal. Not 50-equal as I erroneously stated before. I suppose it is a bit on the large side for a schisma. 5120/5103 is a slightly more petite 5.8 cents. So, there is a payoff for the additional complexity.
In fact, the difference between them is the boring old 5-limit schisma. So, you could use two septimal schismas and forget the 5-limit. Alternatively, you can take off another 5-limit schisma to get (25 -14 0 -1)H or 33554432/33480783. Believe it or not, this seems to be becoming known as "the" septimal schisma. Why? Well, it's a more schisma-sized 3.8 cents. However, take off another 5-limit schisma and we get to 1.9 cents. Now this is surely the ideal septimal schisma. It can be expressed by the matrix (40 -22 -1 -1)H. If you can't understand matrices, though, you'll presumably prefer the ratio 1099511627776/1098337086315.
It doesn't matter which of these septimal schismas you choose, as the outcome is the same: the septimal comma is equal to the other two. Rub me all over with linseed oil if you disagree, but I reckon 225/224 and 5120/5103 are the easiest to remember.
Okay, that's all I've got to say about schismic scales for the time being. Now, I've got another type of scale for you to look at. Good luck!