This page is now supposed to be the one that follows on from the one on meantones. Miracle temperaments are even less well known than schismic so I'll try to assume even less knowledge here.
Melodic Definition of Miracle Scales
Miracle scales fit a 10, rather than 7 or 12, note scale. It consists of 9 small and one slightly larger interval to the octave. The smaller interval is called the secor, after George Secor who discovered miracle temperament, but didn't call it that. I write it as s. The difference between the two intervals I call the quomma, because it's between a quartertone and a comma, and I write it as q. So here's the 10 note "decimal" scale
0 1 2 3 4 5 6 7 8 9 0 s s s s s s s s s s+q
I use numerals to stand for notes because there are 10 of each. 31, 41 and 72 note equal temperaments are all part of the Miracle family. In 31-equal, s is 3 steps and q is 1 step. In 41-equal, s is 4 steps and q is still 1 step. In 72-equal, s is 7 steps and q is 2 steps. The number of steps for an interval in 72-equal is always the sum of the numbers of steps for that interval in 31- and 41-equal. So I won't mention 72 so much from now on.
The next biggest miracle scale is called "Blackjack" and has 21 notes. It can be written like this:
0 1 2 3 4 5 6 7 8 9 0 q r q r q r q r q r q r q r q r q r q r q
Where r=s-q is 2 steps in 31-equal or 3 steps in 41-equal. So now there are more notes than names. We use the symbol > to raise by a quomma and < to lower by a quomma. These are like # and b for meantones. So the start of Blackjack is 0 0> 1 1> 2 2> ...
In meantone, all notes can be defined on a single spiral of fifths. Miracle notes all lie on a spiral of secors. I write it like this:
That's all there is to it.
Approximations to Just Intonation
"Miracle" means Multiple Integer Ratios Approximated Consistently, Linearly and Evenly. So, it's time for the approximations!
The secor is like a diatonic semitone, and could stand for either of the ratios 15:14 and 16:15. A secor plus a quomma is a neutral second, which could be an approximation to 12:11. A secor plus two quommas is a small major second, which could approximate 10:9.
Two secors are a supermajor second, and approximate 8:7. Two secors minus a quomma are a large major second, approximating 9:8. Two secors plus a quomma are a subminor third, approximating 7:6 Two secors minus two quommas are a neutral second, approximating 11:10.
Three secors are a neutral third, or 11:9. Three secors minus a quomma are a 6:5 minor third. Three secors plus a quomma are a 5:4 major third. Three secors plus two quommas are a spuermajor third, approximating 14:11.
Four secors in 31-equal are the same as the meantone wolf. The simplest approximation is to 21:16, although it is also close to 13:10. Four secors minus a quomma are a supermajor third of 9:7. Four secors plus a quomma are a 4:3 perfect fourth.
Five secors are a tritone, approximating 7:5. Five secors minus a quomma are a super fourth of 11:8. Five secors plus a quomma are another tritone, this time 10:9.
Six secors are a perfect fifth (3:2) and so it goes on, but I'll leave it there.
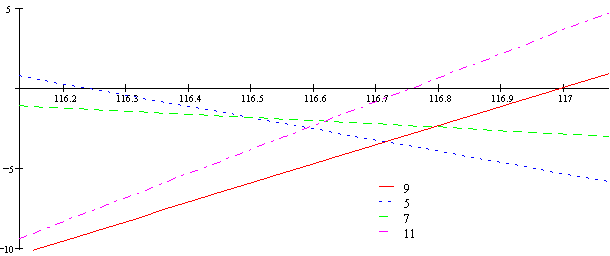
Now, here's the graph showing how close each interval gets to just intonation:

The y (vertical) axis shows how sharp an interval is in cents. The x axis shows the size of the secor in cents. I've shown 9 rather than 3 because that's what you use to compare 11-limit intervals. The left hand edge of the diagram is 31-equal, and the right hand side is 41-equal. 72-equal has a secor of 116.7 cents, which is close to where all the points converge in the middle, and therefore where the best temperaments are.
Here's the miracle conversion matrix:
(1 0)
(1 6)
C = (3 -7)
(3 -2)
(2 15)
That's by octaves and secors, rather than fifths. To get a complete 11-limit chord, you need a string of at least 23 secors. For a complete 5- or 7-limit chord, you need 14 fifths.
It happens that the most complex 11-limit intervals on the spiral of secors are 11:10 and 10:9. That's convenient, because these are also two of the smallest 11-limit intervals (the other being 12:11), and so the ones that cause trouble in chord voicings what with small intervals sounding more dissonant.
I have more pages showing a special lattice for miracle temperaments and more about the notation I use. Or you could move on to schismic scales now.