This page is my attempt to explain everything I can be bothered to about meantone temperament. It's all mathematical one way or another, but most of it isn't that difficult. Skip to the bits that look interesting!
I'm assuming you're au fait with my introduction for tuning neophytes. There are also links to other bits of the sites, but I think this page is fairly self explanatory. If you find you don't understand something, you could always try a link via my meantone website.
Melodic Definition of Meantones
By "melodic definition" I mean the scale is defined in terms of small intervals. Using large, supposedly consonant intervals would be a "harmonic definition". Here's that good old diatonic scale, then:
C D E F G A B C t t s t t t s
The "t" interval can be called a tone, and "s" a semitone. As these words are ambiguous, though, I'll stick to letters in this page.
I don't know a rock solid definition of what is and isn't a meantone. At the least, though, you can expect the t to be a larger interval than the s. Also, the whole of this scale should be some kind of octave. General meantones can then be defined as 5+2 scales. This is my own terminology, and means an octave (whatever that means) consists of 5 large and 2 small intervals.
Although all meantones are 5+2 scales, not all 5+2 scales are meantones. That's the way think of it, anyway. For a tighter definition, then, I prefer to define 12 note meantones as 7+5 scales. Here's an example:
C C# D Eb E F F# G Ab A Bb B C r s s r s r s s r s r s
Here, s and r are both kinds of semitones. As this should be 7 large and 5 small intervals, s should be larger than r. In Pythagorean intonation, s is smaller than r. By my definition, Pythagorean is not a meantone. Other people think differently: it's a matter of taste. There are important cases where Pythagorean scales are treated as if they were meantones.
Fbb-Cbb-Gbb-Dbb-Abb-Ebb-Bbb-Fb-Cb-Gb-Db-Ab-Eb-Bb-F-C-G-D-A-E-B-F#-C#-G#-D#-A#-E#-B#-Fx-Cx-Gx-Dx-Ax-Ex-Bx
That's the meantone spiral of fifths. There's nothing else to it, but I do have more to say about it. Well, I'm not going to end this section here, anyway.
The spiral of fifths is a very common, and useful, way of defining notes within meantone scales. The simplest way to fit a meantone temperament to a fixed pitched instrument is to take a chunk from the cycle of fifths. Often, you take a spiral that almost closes to become a circle. All equal tempered meantones represent a closure of the spiral of fifths. The most common is 12-equal. The 12-equal circle of fifths is sometimes called "the circle of fifths". However, the spiral of fifths is also called a circle. Calling it a spiral emphasizes the fact that it doesn't naturally close.
The simplest, most symmetrical way of choosing a section from the spiral of fifths is to have an equal number of sharps and flats. For 19 notes to the octave, this is:
Cb-Gb-Db-Ab-Eb-Bb-F-C-G-D-A-E-B-F#-C#-D#-G#-A#-E#-B#-Fx-Cx-Gx-Dx-Ax-Ex
When choosing a 12 note meantone, we have a dilemma. There are two different ways of defining 2 notes from the spiral of fifths around D:
Eb-Bb-F-C-G-D-A-E-B-F#-C#-G#
and
Ab-Eb-Bb-F-C-G-D-A-E-B-F#-C#
Whatever you choose, one fifth will be out of tune. This "bad" fifth is called the wolf. You could have the white notes close to a meantone, and average the black notes to get rid of the wolf. This is the key to a lot of well temperaments. For example, Werckmeister III has some intervals between white notes tempered close to 1/4 comma meantone.
Back in the 19th Century, Bosanquet came up with this terminology of linear temperaments. A linear temperament is one defined by a single size of octave and fifth. If the fifth is flat of 7/12 octaves, the temperament is negative. For perfect octaves, this is the same as my definition of meantone as a 7+5 scale, with a few exceptions. The negativeness comes from it being 7 large and 5 small intervals.
Some people define negativeness as being where the fifths is flat of just. This is less useful, IMHO, as it doesn't draw the line between meantone and schismic temperaments.
Before reading this section, be warned that it is of very little importance.
Above, I defined an octave in terms of r and s. I'll now introduce a new interval q=s-r. An octave is 12r+7q.
An equal temperament is double negative if q approximates to 2 steps. If q is one step, the temperament is single negative.
You can always produce a double negative temperament by doubling the number of steps in a single negative temperament. Such scales are not meantones as all notes cannot be reached by a single spiral of fifths.
There are also some double negative temperaments which are meantones.
Some singly negative temperaments are 7, 19, 31, 43, 55 and 67 steps per octave. The difference between each number is 12. So, there are 7+12n steps in a singly negative temperament where n is an integer >= 0. It follows from this that all singly negative temperaments must have an odd number of steps to the octave.
If 7 is single negative, 14 must be double negative. 14 is 12+2. So, there are 2+12n steps in a double negative temperament. It follows that all double negative temperaments must have an even number of steps to the octave. The set is 2, 14, 26, 38, 50, 62, 74, etc. 38 is 19*2 and 62 is 31*2. So, every other double negative temperament is not a meantone. The other ones are. Hence, the double negative meantones have 2+24n steps to the octave.
The concept of double negativity has no meaning for non-equal temperaments. So it isn't a particularly useful way of characterizing meantones. Which is why I said at the top of this section that it isn't very important.
Approximations to Just Intonation
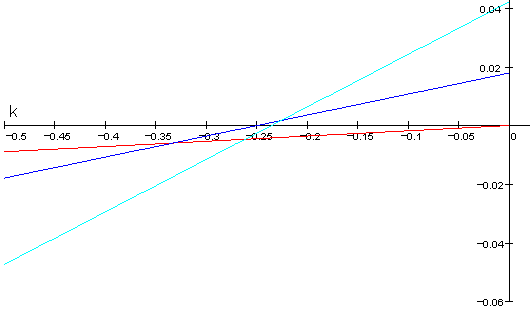
When working with meantone temperaments, you can quite happily forget the overtone series altogether. However, chords will (under some circumstances) sound "purer" the closer you get to JI. So, you may as well know how close you're getting. This is all mathematically involved, but the following graph contains all that your eyes can tell you:

This site includes a similar diagram which, on closer inspection, probably wasn't originally drawn by Robert Smith (he's only credited with one tuning) but is still older than mine. It doesn't include the approximation to 7/4.
The y (vertical) axis shows how sharp an interval is. Don't worry about the units, but be aware that they're the same for all these types of graphs that I'm showing you. The x axis shows the k- in k-comma meantone. So, 1/4 comma meantone has k=-0.25. The closer k gets to zero, the closer the tuning gets to Pythagorean.
The red line shows how sharp the fifth (3/2) is. The blue line shows how sharp the major third (5/4) is. The cyan line shows how sharp the subminor seventh (7/4) is. The minor third (6/5) is out of tune by the difference between the red and blue lines. So, for any "normal" meantone, this graph gives you an idea how out of tune all the intervals are, relative to just intonation.
Note that, at 1/4 comma meantone, the major third is exactly "in tune". And, at 1/3 comma meantone, the minor third is exact. This is illustrated by the red and blue lines crossing. Surprisingly enough, fifths are just in Pythagorean intonation.
There is an infinite number of meantones. However, I'll talk about a few of them to give you an idea of the territory. You should try listening to these to get a feel for them. One way of doing this is to use my MIDI Relay, where you can set k (k3 in fractional mode of "Edit Meantone" and the rest is done for you. I might also get some MIDI files up here sometime.
All opinions are my own. In many cases they are based on little more than a quick try out of each scale. So, don't be afraid to disagree with them.
There ends our tour.
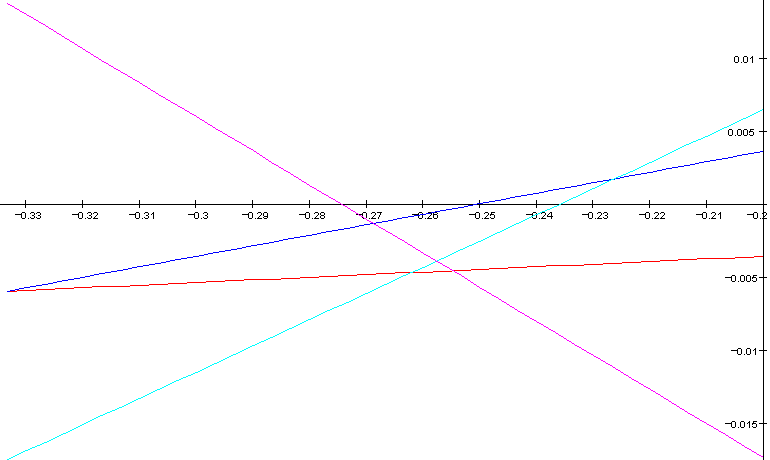
The standard 7-limit approximation works for most meantones. In the 11-limit, it's not so simple, though. There's this:
and this:
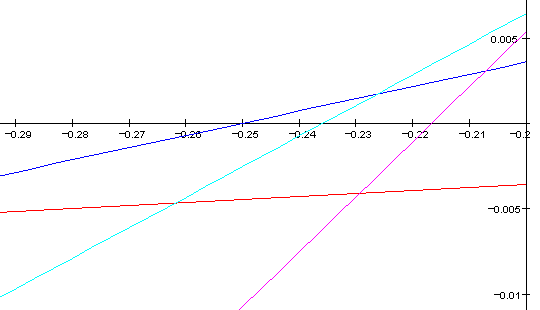
In both cases, the magenta line shows how sharp 11/8 is. The two approximations are equivalent for 31-equal. This is an argument for using 31-equal as your standard 11-limit meantone: it simplifies everything. There's only one neutral third, so it must be 11/9. Otherwise, the second approximation is better for unequal temperaments as you get more chords for fewer notes.
The page on 31-equal tells you how to fit 11-limit intervals intervals to it. for other temperaments, you're on your own...
This is the heaviest mathematical bit, so readers of a delicate constitution may want to skip it.
I've already explained in some detail how to get matrices to work for meantones. That only covered the 5-limit, though. Here's the 11-limit approximation the first of those two graphs above is based on:
( 1 0)
( 0 1)
C = ( -4 4)
(-13 10)
( 24 -13)
Because 11/1 is -13 steps on the spiral of fifths, and 7/1 is +10 steps, 11/7 requires 10--13=23 steps and so you need at least 24 notes in your unequal scale for even one such interval to exist, unless you choose the notes specially. That's why this approximation doesn't give you that many 11-limit chords.
This, then, is the other 11-limit approximation:
( 1 0)
( 0 1)
C = ( -4 4)
(-13 10)
(-25 18)
The 11/1 is further on the spiral of fifths, but its sign is the same as the other prime directions. So, you can get a complete 11-limit chord with only 19 notes to your octave.
Both are so distant that you may as well go for an equal temperament.
If you want to derive these by zeroing intervals, try (1 2 -3 1)H or (-5 2 2 -1)H for the 7-limit. Then, zeroing (-1 2 0 -2 1)H gives you the first 11-limit approximation, and zeroing (2 3 1 -2 -1)H gives the second.
In terms of a meantone H', the intervals mentioned on this page are:
(t) ( -3 2) (s) ( 8 -5) (r) = (-11 7)H' (q) ( 19 -12)
So, now that you've got meantones sussed, have a look at the equivalent page on schismic scales. Go on, you know you want to!