Here's the list of things I've got to say about it:
These are 10+2 scales. That is, 10 large semitones and two small ones to an octave. I'm not sure about the standard mapping, of which more below.
Because the large semitone behaves a bit like the meantone s, and the small one a bit like the meantone r, I'll give them the same names. I hope there's no confusion here, but I'm running out of alternative alphabets!
That's right, 10+2 scales can't be described by a single spiral of fifths. That makes them qualitatively different to meantone and schismic scales. You need two spirals a half-octave apart. One way to fit them to a standard keyboard is to have two independent spirals on the black and white keys. This gives the following layout.
C C# D Eb E F F# G GA A Bb B C s s s s r s s s s s s r
This is founded on the highest principles of symmetry. It is a bit odd, though. C major and A minor don't work in it for a start. And the smallest intervals being between E and F, and B and C? Also, there are different numbers of fifths taken from each spiral.
This is another mapping, but this time with each spiral having 6 fifths.
C C# D Eb E F F# G G# A Bb B C s s r s s s s s r s s s
It does at least have a recognizable diatonic scale in it. Not all chords of C major ar optimized, though. This is another temperament where you have to worry about syntonic commas. The fifths are A-E-B-F#-C#-G# and Eb-Bb-F-C-G-D. Obviously a major tone is 2s, and a minor tone s+r. So, r is the difference between a major and minor third. That means s and r mean similar things to meantone, and we can get away with writing them both the same.
Double positive linear temperaments
The set of double positive temperaments starts 10, 22, 34, 46, 58. These are all diaschismic. However, 94-equal and double positive temperaments thereafter work better as schismic. And, quadruple-positive scales like 56-equal are of this kind. So, calling schismic scales singly positive and these other ones double positive isn't correct in general. It isn't far off, though.
Approximations to Just Intonation
With this kind of temperament, a Pythagorean comma is equal to two syntonic commas. That's why they have to be at least double positive. It also provides the acid test for telling them apart from schismic scales.
If you're not worried about JI, you could describe 22 and 46-equal as schismic. 22-equal comes out as:
C C# D Eb E F F# G GA A Bb B C 1 3 1 1 3 1 3 1 1 3 1 3
If you think it makes sense to have a major tone equal to two minor tones, and a semitone somewhere in the middle well, to you 22-equal is schismic. 46-equal comes out a lot saner, though. The only thing stopping it being schismic is that it approximates JI better this other way.
With non-equal temperaments, the distinction is schismic scales won't have a perfect half-octave.
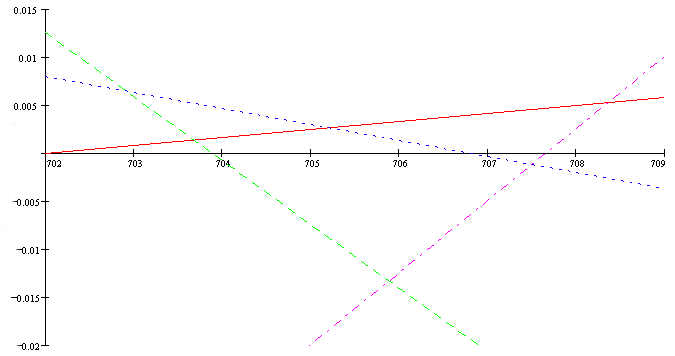
Okay, here's a picture:

That shows the error in the fifth as the solid red line, the error in the major third is the small-dashed blue line, and the error in the 4:7 is the large-dashed green or dot-dashed magenta line. In a crazy unstandard way, the horizontal axis shows the size of the fifth in cents, and the vertical axis shows the size of the error in octaves.
There are two lines for the 4:7 because there are two different 7-limit approximations that cover this standard range. They are equivalent at 34-equal, which is therefore the worst 7-limit temperament on the chart. 46= is towards the left (704.3 cents) and 22-equal is on the right boundary.
46-equal is fairly close to just in the 7-limit. The third is the worst interval. 46 is a lot of notes, but you can use it with a 22 note keyboard mapping. 58-equal is like 46 only more so. It's a nifty 15-limit consistent temperament, and has a fifth of 703.4 cents. The problem is that the 7-limit approximation isn't consistent with 22-equal. So, you won't be putting your fingers where you would if you were playing 22-equal.
34 is inconsistent, but between 34 and 22 there are some quite good 7-limit temperaments. For these, the thirds are good and the fifths not so. 56-equal is close to the optimum here (56=34+22, so it splits the difference of the two extremes) so you can get a handle on it. (It also looks consistent in the 11-limit, although I haven't worked this out properly yet.) As this approximation is consistent with 22-equal, you can happily map 56-equal to a 22 note keyboard.
22-equal isn't that great in the 7-limit. It's economical enough to be very useful, though. Paul Erlich's decatonic scales only work with the 7-limit mapping that is (pretty much) unique to 22-equal.
Really, these temperaments don't look like a single system at all when you get to the 7-limit. That's one reason I don't use them anything like as much as schismic scales. However, they do share considerations in keyboarding. And, you can do quite a bit with 22 notes where you need 29 for schismic scales.
The 5-limit conversion matrix is:
(1 0)
C = (0 1)
(5.5 -2)
The .5 means that you need to have half octaves. You could think of the scales as generated from fifths and half octaves instead of fifths and full octaves. A 5-limit triad can be generated with typically 6 notes to the octave. This is because the span on the right hand column is 3, and you need to double it because of the double octaves.
The matrix is generated by setting the interval (11 -4 -2)H to zero. This is the difference between two syntonic commas of (-4 4 -1)H and a Pythagorean comma of (-19 12 0)H.
For the approximation consistent with 58- and 46-equal, you set (1 2 -3 1)H to zero. That's the difference between an enharmonic diesis (7 0 -3 0)H and a septimal comma (6 -2 0 -1)H. The conversion matrix is:
( 1 0)
( 0 1)
C = ( 5.5 -2)
(15.5 -8)
So, a complete 7-limit chord requires typically an 18 note scale. If we take it to the 15-limit, we need 35 notes for a complete chord, which isn't that bad as 15-limit temperaments go.
( 1 0)
( 0 1)
C = ( 5.5 -2)
(15.5 -8)
(22.5 -12)
(27.5 -15)
The approximation consistent with 56-equal is got by setting the septimal comma (6 -2 0 -1)H equal to the small diesis (-10 -1 5 0)H. That gives the following conversion matrix:
( 1 0)
( 0 1)
C = ( 5.5 -2)
(-11.5 9)
This typically requires a 22 note scale for a complete 7-limit chord. The 22-consistent mapping is generated by setting (1 0 2 -2)H to zero. This is the same as setting 7/5 and 10/7 to be equal. So, this is the only approximation where the half octave actually means anything. Here's the matrix you get:
(1 0)
(0 1)
C = (5.5 -2)
(6 -2)
By far the simplest -- only 6 notes required to get a complete 7-limit chord. But, you'll only ever need 22 notes in your scale as you'll only ever need this if you're using 22-equal or something very similar.